TALLER #1
ACTIVIDAD # 2
GUÍA # 2
REPASO DE NÚMEROS ENTEROS
Observar los siguientes dos vídeos explicativos de como resolver operaciones con números enteros. Para observarlos de clic en la palabra vídeo que aparece en azul.
video 2 multiplicación y división de números enteros.
SUMA Y RESTA DE NÚMEROS ENTEROS
En primer lugar, si lo que tenemos son números con el mismo signo, lo que debemos hacer es sumar los valores y dejar el signo que tengan. Si es positivo (+), el positivo y si es negativo (-), el negativo.
¡Importante!
Si no ponemos nada delante del número se entiende que es positivo (+).
Ejemplo:
(+2) + (+3) = +5
Normalmente lo encontraremos así:
2+3 = 5
(-2) +(-3) = -5
En segundo lugar, si tenemos números con distinto signo, lo que debemos hacer es restar sus valores absolutos y se pone el signo del sumando de mayor valor absoluto. Si tenemos más de dos números, sumamos los del mismo signo por separado y hacemos la resta, dejando el signo del valor de la mayor suma. Lo veremos en el siguiente ejemplo:
(-30) + (+20) =
¿Cómo lo hacemos? 30-20 = 10
¿Cuál es el mayor? El 30, tiene signo negativo, pues dejamos ese signo.
Solución: (-30) + (+20) = -10
Otro ejemplo:
(-20) +(+8) +(-9) =
¿Cómo lo hacemos? Sumamos los del mismo signo y los restamos con el del otro. 20+9 = 29 (signo negativo) y 8 (signo positivo) 29-8 =21
¿Cuál es el mayor? El 29, tiene signo negativo, pues dejamos ese signo.
Solución (-20) +(+8) +(-9) = -21
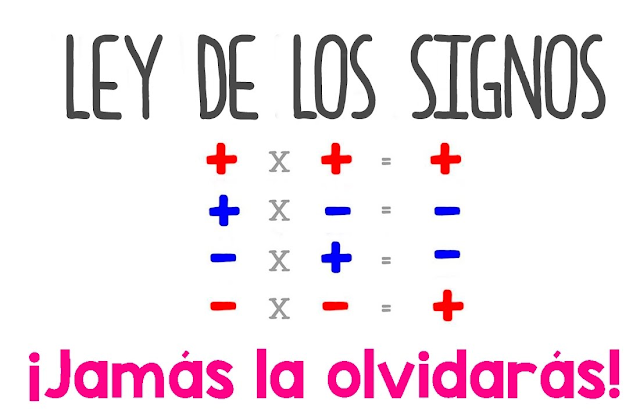
MULTIPLICACIÓN Y DIVISIÓN DE NÚMEROS ENTEROS
Lo primero que debes saber es la ley de signos para poder multiplicar y dividir números enteros.
ACTIVIDAD # 2
Para ejercitar estas operaciones, te dejo una pagina donde aparece ejercicios interactivos, dele clic en la palabra ejercicio que aparece en azul.
EJERCICIO
Debes dar el resultado de la operación que aparece, haz 15 veces este procedimiento con cada numeral ( suma de enteros, resta de enteros, multiplicación de enteros, operaciones combinadas) manda la foto de la calificación de cada enunciado al correo.
GUÍA # 3
LOS NÚMEROS REALES
PRIMERO OBSERVA ESTE VÍDEO
Lee la siguiente historia y contesta las preguntas:
PREGUNTAS
DE ACUERDO AL TEXTO RESPONDE:
1. ¿ COMO SE CONTABA ANTES ?
2¿ COMO SE EXPRESABA CANTIDADES?
3.¿ POR QUE EL 1 ES IMPORTANTE.?
4.¿PORQUE EL 0 ES IMPORTANTE?
5.¿CUALES SON LAS OPERACIONES ARITMÉTICAS?
6.¿ PARA QUE SE UTILIZAN LOS NÚMEROS?
7.¿ QUE OTROS TIPOS DE NÚMEROS MENCIONA LA LECTURA?
8.¿CUAL ES EL MENSAJE QUE DEJA LA LECTURA?
9. DE ACUERDO A LA LECTURA CUALES SON LOS NÚMEROS PRIMOS MENCIONADOS
GUIA # 4
REGLA DE TRES SIMPLE
OBSERVA ESTE VÍDEO
ACTIVIDAD #4
CON BASE A LOS EJEMPLOS RESUELVE
GUÍA # 5
MÍNIMO COMÚN MÚLTIPLO ( MCM )
OBSERVA EL VÍDEO
Múltiplos de un número
Se llama múltiplo de un número al resultado de multiplicar ese número por cualquier otro número natural. Como los números naturales son infinitos, los múltiplos de un número también son infinitos.Son múltiplos de 5: 5, 10,15, 20, 25, 30… ya que resultan de multiplicar el 5 por el resto de números naturales:5 x 1 = 55 x 2 = 105 x 3 = 155 x 4 = 20De esta forma, se pueden obtener los múltiplos de cualquier número:Múltiplos de 3: 3, 6, 9, 12, 15, 18, 21, 24, 27 ….Múltiplos de 9: 9, 18, 27, 36, 45, 54, 63 ….Recuerda: Los múltiplos de un número, siempre son mayores que ese número
El mínimo común múltiplo de 2 o más números es el múltiplo que sea común para esos números y además es el más bajo. Por ejemplo, vamos a verlo con el 3 y el 9:
Múltiplos de 3: 3, 6, 9, 12, 15, 18, 21, 24, 27 ….
Múltiplos de 9: 9, 18, 27, 36, 45, 54, 63 ….
Vemos que tienen en común como múltiplos el 9, el 18, el 27… El más pequeño de todos ellos es el 9, por tanto, ese será el mínimo común múltiplo de 3 y 9.
Se utiliza para calcular el mínimo común denominador, a la hora de sumar o restar fracciones.
El método para calcular el mínimo común múltiplo más directamente es el siguiente:
1 – Se descomponen los números en factores primos.
2- Se seleccionan todos los factores que aparezcan al descomponer los números, comunes y no comunes, elevados al mayor exponente
3 – Se multiplican los factores elegidos (con el exponente elegido para cada uno) y el resultado será el mínimo común múltiplo
Ejercicio resuelto 1
Utilizaremos el mismo ejemplo que antes. Vamos a calcular el mínimo común múltiplo de 3 y 9, que se escribe así:
m.c.m. (3 y 9)
1 – Primero descomponemos los números. El 3 no hace falta, ya que es primo.
Por tanto descomponemos el 9:
2 – Después elegimos los factores. Escribimos 3 y 9 pero descompuestos en factores primos:
3 = 3
9 = 3²
Como único factor tenemos el 3.
El máximo exponente al que está elevado es a 2.
Por tanto, se queda como 3².
Por último, realizamos la potencia:
Veamos otro ejemplo algo más complicado. Hallar el mínimo común múltiplo de 6, 12 y 30.
Primero, descomponemos en factores primos: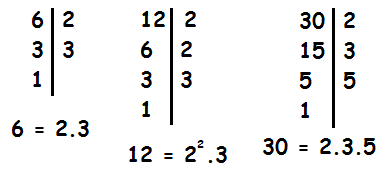
Ahora elegimos los factores:
Tenemos el 2, el 3 y el 5.
El mayor exponente que aparece para el 2 es a 2. El 3 y 5 están elevados a 1.
Por tanto, elegimos 2² 3 y 5.
En el último paso, volvemos a realizar las potencias y multiplicamos:
Ejercicio resuelto 2Calcular el mínimo común múltiplo de 4, 24 y 361 – Se descomponen los números en factores primos: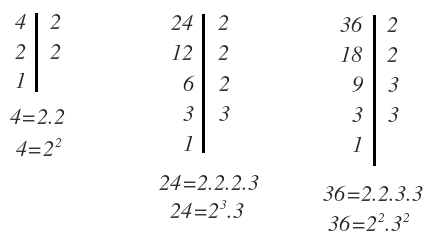
2 – Elegimos los factores comunes y no comunes. En el 4 tenemos un 2, en el 24 tenemos un 2 y un 3 y en el 36 otro 2 y otro 3. Vamos a poner las 3 descomposiciones juntas para verlo más claro:
Por tanto los factores elegidos son 2 y 3.Ahora vamos a elegir los exponentes, que será el mayor para cada uno:El 2 lo tenemos elevado a 2 y a 3, por tanto nos quedamos con el 3El 3 lo tenemos elevado a 1 y a 2, por tanto nos quedamos con el 2Los factores elevados a sus mayores exponentes serían 2³ y 3².
El m.c.m. de 4, 24 y 36 es la multiplicación de estos factores con sus exponentes:
ACTIVIDAD # 5
GUÍA # 6
FRACCIONES
SUMA DE FRACCIONES
HOMOGÉNEAS
Cuando las fracciones que quieras sumar tienen el mismo denominador, la operación es muy simple: El denominador se conserva y solo hay que sumar los dos numeradores:
HETEROGÉNEAS
Y ESTOS MISMOS PROCESOS SE HACEN PARA LA RESTA SOLO QUE NO SE SUMA SINO QUE SE RESTA
HOMOGENAS
HETEROGÉNEAS
ACTIVIDAD # 6
RESUELVE
GUÍA # 7
MULTIPLICACIÓN Y DIVISIÓN DE FRACCIONES
Multiplicación
DIVISIÓN
EJEMPLOS
ACTIVIDAD # 7
GUÍA # 8
SUMA Y RESTA DE UN ENTERO CON UNA FRACCION
SUMA
OBSERVA EL VÍDEO
RESTA
OBSERVA EL VIDEO
EL MISMO PROCESO QUE SE HACE PARA LA SUMA SE HACE PARA LA RESTA
CLASIFICACIÓN DE NÚMEROS DECIMALES.
OBSERVA EL VÍDEO
ACTIVIDAD# 9
1. Realiza la división y Di a qué tipo de número decimal corresponden:
GUÍA # 10
Todo número decimal tiene su equivalente en forma de fracción. La fracción que genera un número
decimal se llama "Fracción Generatriz".
Caso I: "Cuando el número decimal es exacto o limitado"
Caso II: "Cuando el número decimal es periódico puro."
Caso III: "Cuando el número decimal es periódico mixto".
ACTIVIDAD # 10
GUÍA # 11
ACTIVIDAD # 11
ESCRIBE LA FRACCIÓN QUE CORRESPONDE A CADA GRÁFICA Y LUEGO REPRESENTARLAS EN LA RECTA NUMÉRICA.
GUIA # 12
´PRODUCTO CARTESIANO
ACTIVIDAD # 12
GUIA # 13
PAREJAS ORDENADAS EN EL PLANO CARTESIANO
ACTIVIDAD # 13
GUÍA # 14
INTRODUCCIÓN AL ÁLGEBRA
ACTIVIDAD# 14
DE ACUERDO AL TEXTO ANTERIOR RESPONDE
GUIA # 15
ECUACIONES
RECORDEMOS
ACTIVIDAD # 15
RESUELVE LAS SIGUIENTES ECUACIONES
GUIA# 16
CLASIFICACION DE POLINOMIOS
ACTIVIDAD # 16
GUIA # 17
TERMINOS SEMEJANTES
Los términos semejantes son aquellos que tienen la misma parte literal, o dicho de otra forma aquellos que tengan las mismas letras y con igual exponente. Ejemplo: y son términos semejantes, además y también son términos semejantes, pues su parte literal es decir es la misma.
ACTIVIDAD # 17
GUIA # 18
SUMA Y RESTA DE MONOMIOS
ACTIVIDAD # 18
RESUELVE
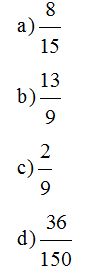
Profe como me puedo comunicar con usted soy camilo de octavo
ResponderBorrarProfe q vamos hacer no entiendo
ResponderBorrarEste comentario ha sido eliminado por el autor.
ResponderBorrar