INSTRUCTIVO # 1
TALLER #1
ACTIVIDAD # 2
INSTRUCTIVO # 3
NÚMEROS NATURALES EN EL PLANO CARTESIANO
Cada punto en el plano cartesiano puede representarse con
un par ordenado de números (x, y).
PAR ORDENADO:
Sea el par ordenado ( 3; 5 ); 3 es el
primer elemento y 5 es el segundo elemento.
Así mismo, son pares ordenados:
(
5; 3 ), ( 6; 0 ), ( 0; 8 ), ( 2; 5 ), etc.
Un par ordenado representa un punto en el plano cartesiano.
Así:
ACTIVIDAD # 3
INSTRUCTIVO # 4
POTENCIACIÓN
PRIMERO OBSERVA ESTE VÍDEO
ACTIVIDAD # 4
INSTRUCTIVO # 5
RADICACION
ACTIVIDAD #5
INSTRUCTIVO # 6
NÚMEROS PARES E IMPARES

INSTRUCTIVO # 7
MULTPLOS Y DIVISORES
ACTIVIDAD # 7
INSTRUCTIVO # 8
NÚMEROS PRIMOS Y COMPUESTOS
ACTIVIDAD # 8
INSTRUCTIVO # 9
CRITERIOS DE DIVISIBILIDAD
ACTIVIDAD # 9
1. COMPLETA EL SIGUIENTE CUADRO
2.
INSTRUCTIVO # 10
ACTIVIDAD # 10
INSTRUCTIVO # 11
SUMA Y RESTA DE FRACCIONES
Suma y resta de fracciones con igual denominador
Es muy fácil hacer la adición de fracciones con igual denominador, debido a que en este caso agregamos partes de objetos del mismo tipo. En este apartado vamos a estudiar cómo hacer esta operación de forma gráfica, en la recta numérica y de manera analítica.
Vamos a sumar 15 + 35 .
Lo primero que haremos será representar gráficamente las fracciones.
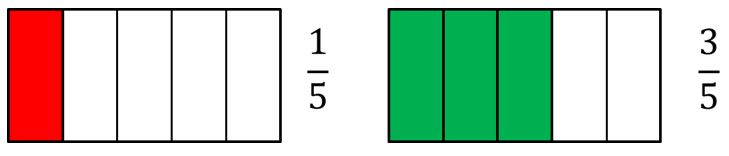
Ahora juntemos las porciones de la unidad representadas en color rojo y verde. Recuerda que es posible unir estas porciones, porque ambas fracciones están denominadas en quintos.
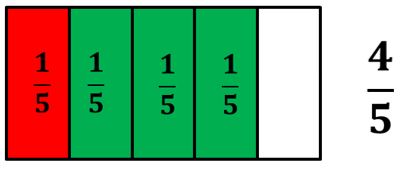
Al juntar las fracciones 15 y 35 se obtiene como resultado 45 . Es decir, que:
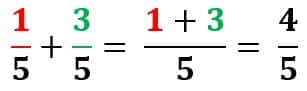
Para sumar fracciones de igual denominador se suman los numeradores y se conservan los denominadores.
SUMA DE FRACCIONES CON DIFERENTE DENOMINADOR
RESTA DE FRACCIONES
Para restar fracciones se hace el mismo proceso anterior, el que se realizo para la suma.
ACTIVIDAD # 11
INSTRUCTIVO # 12
MULTIPLICACIÓN Y DIVISIÓN DE FRACCIONES
Para multiplicar dos fracciones, simplemente multiplica los numeradores para obtener el numerador del producto y multiplica los denominadores para obtener el denominador del producto.
Para dividir dos fracciones, primero debes hallar el recíproco del divisor. Esto significa que debes dar vuelta la segunda fracción. Luego, multiplica los numeradores y multiplica los denominadores.
Escribe estos apuntes en tu cuaderno.
Multiplica los numeradores y los denominadores.
ACTIVIDAD # 12
Instructivo 13
PARTE ENTERA Y PARTE DECIMAL
Cada número decimal consta de una parte entera y una parte decimal que van separadas de una coma. La parte entera va a la izquierda de la coma, y puede incluir el cero. La parte decimal va a la derecha de la coma.
Por ejemplo, en el número decimal 1,3 la parte entera es 1 y la parte decimal es 3.
El primer paso es entender que la barra en una fracción significa división o “dividido por”. Por ejemplo, la fracción 3/4 significa en realidad 3 dividido por 4. También tienes que recordar que el número de arriba en una fracción se llama numerador y el número de abajo se llama denominador. En nuestro ejemplo de 3/4, el numerador es 3 y el denominador es 4.
Para convertir una fracción a un número decimal divides el numerador entre el denominador. En nuestro ejemplo del paso anterior, para cambiar la fracción ¾ a decimal, calculamos 3 dividido por 4. El resultado es 0,75. Este es el número decimal que es equivalente a la fracción ¾.
ACTIVIDAD #13
INSTRUCTIVO # 14
ACTIVIDAD # 14
INSTRUCTIVO # 15
SUMA Y RESTA CON NÚMEROS DECIMALES
SUMA
Resta
Se coloca el sustraendo debajo del minuendo de modo que las comas decimales queden en columna añadiendo ceros si es necesario para que el minuendo y el sustraendo tengan igual número de cifras decimales. Se restan como números enteros y se coloca la coma en columna con los demás puntos.
ACTIVIDAD # 15
INSTRUCTIVO # 16
MULTIPLICACIÓN DE DECIMALES
Paso 1
Como en el caso anterior, lo primero es colocar los dos números de modo que el factor más largo esté arriba y el más corto, debajo.
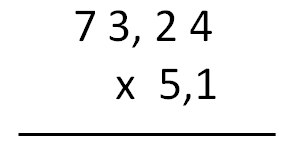
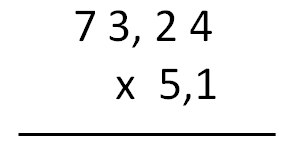
Paso 2
Resolvemos la multiplicación como hacemos normalmente con números enteros. Después, contamos las cifras que hay después de las comas de los dos factores. El resultado debe tener tantas cifras decimales como los dos factores juntos.
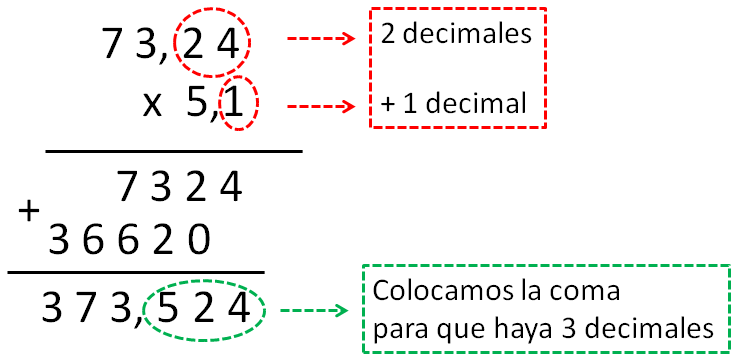
































































no e terminado porque mi celular estaba dañado
ResponderBorrar