INSTRUCTIVO # 1

POLIGONOS

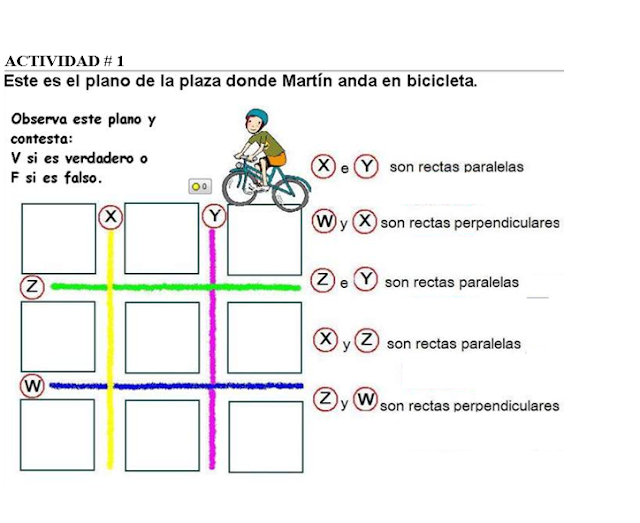
ACTIVIDAD # 1

INSTRUCTIVO # 2

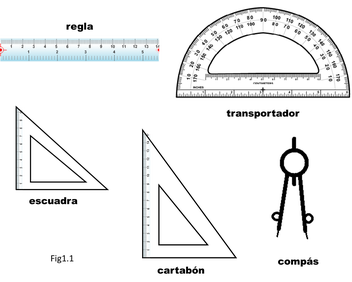
MATERIALES QUE SE UTILIZAN EN GEOMETRIA

COMO SE USAN

ACTIVIDAD # 2

UTILIZA TU REGLA Y DIBUJA LOS SIGUIENTES POLIGONOS

UN CUADRADO CON SUS LADOS DE 4 CM
REALIZA UN RECTANGULO DE 7 CM Y 5 CM
UN TRIANGULO CON UN LADO DE 3 CM

UTILIZA COMPAS PARA REALIZAR UN DIBUJO CON SOLO CIRCULOS COMO EL SIGUIENTE

INSTRUCTIVO # 3

ACTIVIDAD # 3

INSTRUCTIVO # 4

MULTIPLICACIÓN POR 10, 100, 1000

ACTIVIDAD # 4

INSTRUCTIVO # 5

HISTORIA DE LAS MEDIDAS DE LONGITUD (METRO)

Desde la antigüedad, se han elegido las unidades de medida de forma arbitraria. Varias de estas unidades han sido derivadas de eventos naturales y se ha tratado de que sea de fácil manejo y comprensión. Asi, los cuerpos celestes proporcionaron una manera sencilla de calcular el tiempo: el día era el tiempo que transcurría de amanecer a amanecer; el mes, era el tiempo que transcurría entre una cierta fase de la luna y su recurrencia; el año, el tiempo que toma el sol pasar a través de sucesivos cambios de una posición en el ciclo a la misma posición.

Las distancias cortas eran medidas por el número de pasos que tomaba cubrir la distancia y las distancias largas eran medidas por el número de días de travesía. Tazones y tazas eran utilizados para medir la capacidad de recipientes. Granos de trigo y cebada eran utilizados para medir peso de objetos de valor. Por miles de años, el trueque fue el medio de cambio, y así no fue necesario usar unidades de monedas.

Ahora bien, mientras el hombre vivía en comunidades aisladas, casi no existía comercio ni industrias y por tanto no era tan necesario establecer unidades de medida. Sin embargo, cundo el hombre comenzó a trabajar en grupos, se incrementó el comercio entre ellos y esto indujo el establecimiento de unidades de medida que tuvieran el mismo significado para diversas comunidades.

Al principio se establecían unidades para regiones de un mismo país; luego para un país entero y por último, para grupos de países. Se piensa que los romanos fueron los primeros en establecer unidades de medidas ampliamente aceptables. Sin embargo, con la caída del Imperio Romano, estas unidades fueron desechadas. Es importante destacar que el sistema métrico establecido a finales del siglo XVIII, en Francia, es utilizado casi mundialmente en ciencias e ingeniería; solo en algunos países de habla inglesa no lo utilizan para comercio.

A continuación algunas unidades de medida y la costumbre de utilizar el cuerpo humano como base para elegirlas.

Una de las primeras unidades de medidas de longitud fue el cubito, que fue definido como la longitud del antebrazo desde el codo hasta el extremo del dedo medio. El cubito fue utilizado por los babilonios y los egipcios, aproximadamente 2600 años antes de Cristo. El Arca de Noé, según la Biblia, fue construido con las siguientes dimensiones: 300 cubitos de longitud, 50 cubitos de ancho y 30 cubitos de alto.

Otra unidad de medida, el pie, fue utilizado por los griegos y romanos. Fue definido como 2/3 de un cubito y llega a Inglaterra al ser ésta conquistada por los romanos.

El pie fue subdividido por los griegos en doce partes; cada parte al ancho de la uña del pulgar. Cada parte fue llamada por los romanos unicae y mas tarde llamada por los anglosajones pulgadas. Ya que los hombres no tienen el dedo pulgar de igual ancho, el rey Eduardo II, en el siglo XIV, define la pulgada como la longitud de tres granos de maíz tomados del centro de una mazorca

Otra unidad de medida, la yarda, fue creada por los comerciantes de ropa ingleses. Al principio fue definida como la distancia del centro del pecho al extremo de los dedos de un brazo extendido (mitad de una “brazada”). El rey Enrique I, quien gobernó a Inglaterra en 1100, define la yarda legal como la distancia del extremo de su nariz al extremo del dedo pulgar de su brazo extendido.

Para medir pesos, los babilonios usaban piedras seleccionadas y conservadas para ese propósito. Los egipcios y los griegos usaban semillas de trigo como la menor unidad de peso. La uniformidad de peso de las semillas de trigo hizo de este grano una buena unidad de medida. Esto induce a que mas tarde se definiera la libra como 7.000 granos de trigo.

Los ejemplos anteriores nos ayudan a ver como las unidades de medidas son originadas en forma arbitraria. Pero, es bueno aclarar que muchas de esas unidades de medida son utilizadas hoy día, a pesar de que ellas han sido reemplazadas por unidades de medidas mas precisas.

De allí, entonces la importancia de dichas unidades de medidas en las actividades que realiza el hombre en una sociedad.

La historia del metro como unidad de longitud empezó cien años antes. En la Revolución francesa de 1789, junto a otros desafíos considerados necesarios para los nuevos tiempos, se nombraron Comisiones de Científicos para uniformar los pesos y medidas, entre ellos la longitud. La tarea fue ardua y complicada

Actualmente para medir longitudes se utiliza el metro y sus divisores. Sin embargo, hace tan sólo 200 años, la palabra metro no tenía ningún significado.

La forma de definir y medir una longitud ha cambiado a través de la historia: las primeras referencias utilizadas fueron partes del cuerpo humano; posteriormente, para medir se utilizaban otras unidades como la vara, que tenían longitudes diferentes según el lugar geográfico. Debido a esta falta de uniformidad, gobiernos y monarquías de diferentes países efectuaron varios intentos de unificación.

El 19 de marzo de 1791, la Academia de Ciencias de París propuso la adopción de un patrón procedente de la naturaleza: el metro. Si se aceptaba la propuesta, el metro sería la diezmillonésima parte del cuadrante de un meridiano terrestre. Ante la imposibilidad de medir todo un cuarto de meridiano desde el polo Norte al Ecuador, la solución era medir un trozo y calcular matemáticamente el valor del total. El arco de meridiano escogido en la propuesta de la academia fue el comprendido entre Dunkerque y Barcelona.

Luis XVI encargó a los topógrafos Pierre François André Méchain y Jean Baptiste Joseph Delambre llevar a cabo la medición del meridiano.

La técnica a utilizar sería la de la triangulación geodésica. Se trazaría una cadena de triángulos, los vértices de los cuales serían montañas situadas a lo largo del meridiano y se calcularía sus dimensiones a partir de la medición de dos bases, cuidadosamente medidas sobre la medida del patrón más perfecto que existía en Francia: la toesa.

Después de las mediciones de campo, se efectuaron durante seis meses los trabajos necesarios para determinar matemáticamente la longitud de la diezmillonésima parte del cuadrante del meridiano de París, el metro, y los patrones de capacidad.

Después de largos cálculos, se decidió que el metro, mediría 3 pies de rey, 11 líneas y 296 milésimas de una línea. Una toesa francesa de seis pies valdría 1,9490366 metros.

Una ley de la República Francesa del 10 de diciembre de 1799, firmada por el primer cónsul, Napoleón Bonaparte, establecía el metro para siempre con el lema: “Para todos los pueblos y para todos los tiempos”. Había nacido el metro y el sistema métrico decimal.

ACTIVIDAD # 5

PREGUNTAS

1¿ QUE ES MEDIR?

2.¿COMO MEDIAN EN UN TIEMPO ATRAS?

3.MENCIONE ALGUNAS UNIDADES DE LONGITUD VISTAS EN LA LECTURA.

INSTRUCTIVO #6

MULTIPLICACIÓN Y DIVISIÓN DECIMAL CON POTENCIAS DE 10( 10, 100,1000)

Multiplicar números decimales por 10, 100, 1000…

Para multiplicar un número decimal por 10, 100, 1000… lo único que tendremos que hacer es mover la coma del decimal a la derecha tantas posiciones como ceros tenga el número.

Por ejemplo: Números decimales

Como el 100 tiene dos ceros moveremos la coma dos posiciones a la derecha. Por lo tanto, el resultado es 315,4

EJEMPLO: multipliquemos
34,67 x 1000 = ?
Como el número decimal solo tiene 2 cifras decimales y necesito mover la como 3 lugares, entonces agrego un cero para completar el número de cifras.34,67 x 1000 = 34670

Dividir números decimales por 10, 100, 1000…

Para dividir un número decimal por 10, 100, 1000… lo único que tendremos que hacer es mover la coma del decimal a la izquierda tantas posiciones como ceros tenga el número.

Por ejemplo: