MATEMATICAS SEPTIMO 2021

 

INSTRUCTIVO # 1 NÚMEROS RELATIVOS

TALLER # 1

INSTRUCTIVO# 2 NÚMEROS ENTEROS 

NOTA: LEER BIEN ESTA GUÍA ANTES DE RESOLVER LA ACTIVIDAD.

EJEMPLO 

NUMEROS ENTEROS EN LA RECTA NÚMERICA

 

ACTIVIDAD # 2 

INSTRUCTIVO  # 3 

OPERACIONES CON NÚMEROS ENTEROS 

PRIMERO OBSERVA ESTOS  VÍDEO

suma y resta de números enteros

SUMA Y RESTA DE NÚMEROS ENTEROS 

En primer lugar, si lo que tenemos son números con el mismo signo, lo que debemos hacer es sumar los valores y dejar el signo que tengan. Si es positivo (+), el positivo y si es negativo (-), el negativo.

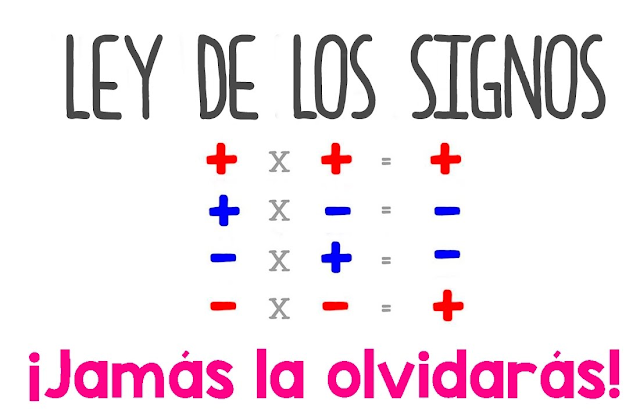
¡Importante!

Si no ponemos nada delante del número se entiende que es positivo (+).

Ejemplo:

(+2) + (+3) = +5

Normalmente lo encontraremos así:

2+3 = 5

(-2) +(-3) = -5

En segundo lugar, si tenemos números con distinto signo, lo que debemos hacer es restar sus valores absolutos y se pone el signo del sumando de mayor valor absoluto. Si tenemos más de dos números, sumamos los del mismo signo por separado y hacemos la resta, dejando el signo del valor de la mayor suma. Lo veremos en el siguiente ejemplo:

(-30) + (+20) =

¿Cómo lo hacemos? 30-20 = 10

¿Cuál es el mayor?  El 30, tiene signo negativo, pues dejamos ese signo.

Solución: (-30) + (+20) = -10

Otro ejemplo:

(-20) +(+8) +(-9) =

¿Cómo lo hacemos? Sumamos los del mismo signo y los restamos con el del otro. 20+9 = 29 (signo negativo) y 8 (signo positivo) 29-8 =21

¿Cuál es el mayor?  El 29, tiene signo negativo, pues dejamos ese signo.

Solución (-20) +(+8) +(-9) = -21

MULTIPLICACIÓN Y DIVISIÓN DE NÚMEROS ENTEROS

Lo primero que debes saber es la ley de signos para poder multiplicar y dividir números enteros.

ACTIVIDAD # 3

RESUELVE 

INSTRUCTIVO # 4

Potenciación de números enteros

Observa el vídeo

ACTIVIDAD #4

INSTRUCTIVO # 5  

RADICACION Y LOGARITMACION 

RADICACIÓN

OBSERVA   EL VÍDEO

LOGARITMACION 

OBSERVA EL VÍDEO 

ACTIVIDAD # 5

INSTRUCTIVO # 6

¿Qué es una fracción?

Una fracción representa el número de partes que cogemos de una unidad que está dividida en partes iguales. Se representa por dos números separados por una línea de fracción.

Términos de una fracción

Los términos de una fracción son el numerador y el denominador. El numerador es el número de partes que tenemos y el denominador es el número de partes en que hemos dividido la unidad.

Vamos a ver un ejemplo: Tenemos diferentes figuras y cada una de ellas la dividimos en diferentes partes iguales, que es el denominador. La parte coloreada es el numerador.

¿Cómo se leen las fracciones?

El numerador se lee con los números cardenales. 1 – un, 2 – dos, 3 – tres, …, 10 – diez, …, 24 – veinticuatro…

El denominador se lee con los números partitivos. 2 – medios, 3 – tercios, 4 – cuartos, 5 – quintos, 6 – sextos, 7 – séptimos, 8 – octavos, 9 – novenos, 10 – décimos. A partir del 11, el número se lee terminado en -avos: 11 – onceavos, 12 – doceavos, …

 

ACTIVIDAD # 6

 

Escribe la fracción que corresponde a cada uno de los dibujos

 

INSTRUCTIVO # 7

NÚMEROS FRACCIONARIOS EN LA RECTA NUMERICA 

 

Representar fracciones en la recta numérica

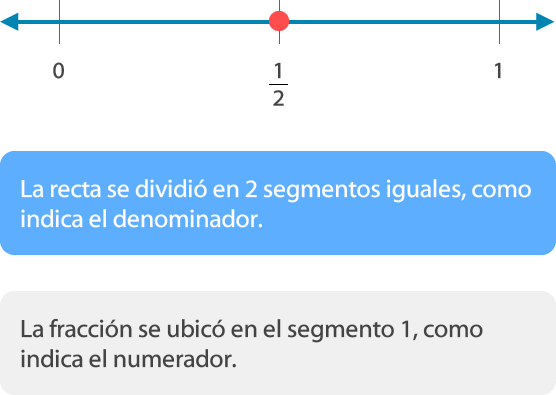
Para ubicar fracciones en la recta numérica se divide la unidad (entero) en segmentos iguales, como indica el denominador, y se ubica la facción según indica el numerador.

Ejemplo de fracciones unitarias (con numerador 1) en la recta numérica:

 

a. Ubicar la fracción  $\frac{\mathrm{1/}}{2}$

 

 B  Ubicar la fracción  $\frac{}{}$1/5

 

Como puedes observar las fracciones unitarias se ubican en el primer segmento de la recta numérica.
 

¿Cómo ubicar fracciones que no son unitarias?
Para ubicar fracciones que no son unitarias en la recta numérica se realiza el mismo procedimiento anterior, es decir, se divide el entero en partes iguales según lo que indique el denominador de la fracción. Luego, se ubica la fracción en el segmento que está señalado en el numerador.

ACTIVIDAD # 7

INSTRUCTIVO#8

FRACCIONES PROPIAS E IMPROPIAS

FRACCIONES PROPIAS E IMPROPIAS. Una fracción se llama propia si su numerador es menor que su denominador. Una fracción se llama impropia si su numerador es mayor que su denominador

ACTIVIDAD #8

INSTRUCTIVO # 9

NÚMEROS RACIONALES

FRACCIONES EQUIVALENTES

SIMPLIFICACIÓN

OBSERVA EL VÍDEO

AMPLIFICACIÓN 

OBSERVA EL VÍDEO

ACTIVIDAD # 9

INSTRUCTIVO # 10

M C M ( MÍNIMO COMÚN MÚLTIPLO) Y M C D ( MAXIMO COMÚN DIVISOR)

observa los vídeos

 

MÍNIMO COMÚN MÚLTIPLO  ( M C M )

¿Qué es el mínimo común múltiplo?

El mínimo común múltiplo de dos o más números es el múltiplo más pequeño que esos números tienen en común.

El mínimo común múltiplo se suele expresar con las siglas m.c.m. (a, b), siendo a y b los números.

¿Cómo se calcula el mínimo común múltiplo, m.c.m?

Vamos a aprenderlo con un ejemplo, calculamos el mínimo común múltiplo de 180 y 324.

m.c.m. (180,324) Para calcular el mínimo común múltiplo de dos o más números, empezamos por descomponer esos números en factores primos. El mínimo común múltiplo se obtiene cogiendo todos los factores (comunes y no comunes), elevados a la máxima potencia. Es decir cogemos todos los factores, pero los que se repitan los cogemos elevados a la máxima potencia. m.c.m. (180,324)= 22x5x34 El 2 aparece como factor primo en ambas descomposiciones, en ambos casos está elevado a 2. El 5 sólo aparece en la descomposición de 180, pero tenemos que coger todos. El 3 aparece como factor en ambas descomposiciones, pero cogemos el denominador más elevado. Hacemos la multiplicación y obtenemos el mínimo común múltiplo. m.c.m. (180,324)= 2 X 2 X 5 X 3X 3 X 3 X 3= 1620 MÁXIMO COMÚN DIVISOR (M C D) El máximo común divisor de dos o más números es el número más grande por el que se pueden dividir dichos números. El máximo común divisor se suele expresar con las siglas M.C.D. (a,b), siendo a y b los números. ¿Cómo se calcula el máximo común divisor (M.C.D)? Vamos a aprenderlo con un ejemplo, calculamos el máximo común divisor de 180 y 324. M.C.D. (180,324) 1. Para calcular el máximo común divisor de dos o más números, empezamos por descomponer esos números en factores primos. 2. El máximo común divisor se obtiene cogiendo solo los factores primos comunes a los números que hemos descompuesto, elevados al menor exponente. Es decir cogemos solo los factores comunes y los que se repitan los cogemos elevados a la mínima potencia. M.C.D. (180,324)= 22x32 El 2 aparece como factor primo en ambas descomposiciones, en ambos casos está elevado a 2. El 3 aparece también como factor común pero en este caso cogemos elevado a la mínima potencia. El 5 no le cogemos porque no es un factor común. 3. Hacemos la multiplicación y obtenemos el máximo común divisor M.C.D. (180,324)= 2X 2 X 3X 3= 36

ACTIVIDAD # 10

INSTRUCTIVO # 11

SUMA Y RESTA DE FRACCIONES 

OBSERVA LOS VÍDEOS 

SUMA DE FRACCIONES 

HOMOGÉNEAS

Cuando las fracciones que quieras sumar tienen el mismo denominador, la operación es muy simple: El denominador se conserva y solo hay que sumar los dos numeradores:

HETEROGÉNEAS

RESTA DE FRACCIONES

Para restar fracciones se hace el mismo proceso anterior, el que se realizo para la suma.

ACTIVIDAD # 11

RESUELVE

1.

A)

72

  - 

53

  = 

B)

32

  -

54

  = 

C)

34

  -

35

  = 

D)

66

  -

22

 = 

2.

INSTRUCTIVO # 12

MULTIPLICACIÓN Y DIVISIÓN DE FRACCIONES

ACTIVIDAD # 12

INSTRUCTIVO # 13

"FRACCIÓN A DECIMAL"

¿COMO CONVERTIR UNA FRACCIÓN A DECIMAL?

Pasos a seguir:

1

El primer paso es entender que la barra en una fracción significa división o “dividido por”. Por ejemplo, la fracción 3/4 significa en realidad 3 dividido por 4. También tienes que recordar que el número de arriba en una fracción se llama numerador y el número de abajo se llama denominador. En nuestro ejemplo de 3/4, el numerador es 3 y el denominador es 4.

2

Para convertir una fracción a un número decimal divides el numerador entre el denominador. En nuestro ejemplo del paso anterior, para cambiar la fracción ¾ a decimal, calculamos 3 dividido por 4. El resultado es 0,75. Este es el número decimal que es equivalente a la fracción ¾.

3 Esta es una situación diferente que se puede producir al convertir una fracción a un decimal. Tienes la fracción 1/3. Cuando utilizamos nuestro procedimiento de dividir 1 entre 3 se obtiene un número decimal que no se detiene. Si utilizas una calculadora para hacer la división verás 0.333333333 que aparece como resultado. Si haces la división a mano, con lápiz y papel, te darás cuenta de que sigues escribiendo 3 en cada paso de la división. Esto se llama un numero periódico. El período se puede expresar escribiendo un arco encima de las cifras repetidas o 0,333… Ambas anotaciones significan que el 3 se repite indefinidamente

PARA TRANSFORMAR UNA FRACCIÓN CUALQUIERA A DECIMAL HAY QUE HACER UNA DIVISIÓN, EXISTE UNA CLASIFICACIÓN DE LOS DECIMALES ESO LO VEREMOS.

OBSERVEMOS EL SIGUIENTE VÍDEO

Luego de saber como se convierte una fracción en decimal, veamos cuales son las clases de decimales.

Observa el siguiente vídeo

ACTIVIDAD#13

Para realizar este punto puedes utilizar calculadora

INSTRUCTIVO  # 14

SUMA Y RESTA CON NÚMEROS DECIMALES

SUMA 

Se colocan los sumandos unos debajo de los otros de modo que las comas decimales queden en columna, se suman como números enteros poniendo en el resultado la coma de modo que quede en columna con los sumandos.

Resta

Se coloca el sustraendo debajo del minuendo de modo que las comas  decimales queden en columna añadiendo ceros si es necesario para que el minuendo y el sustraendo tengan igual número de cifras decimales. Se restan como números enteros y se coloca la coma en columna con los demás puntos.

ACTIVIDAD # 14

INSTRUCTIVO # 15

MULTIPLICACIÓN DE DECIMALES

Paso 1

Como en el caso anterior, lo primero es colocar los dos números de modo que el factor más largo esté arriba y el más corto, debajo.

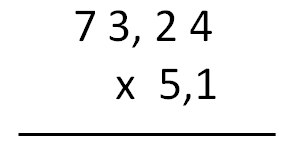
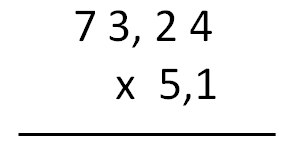
Paso 2

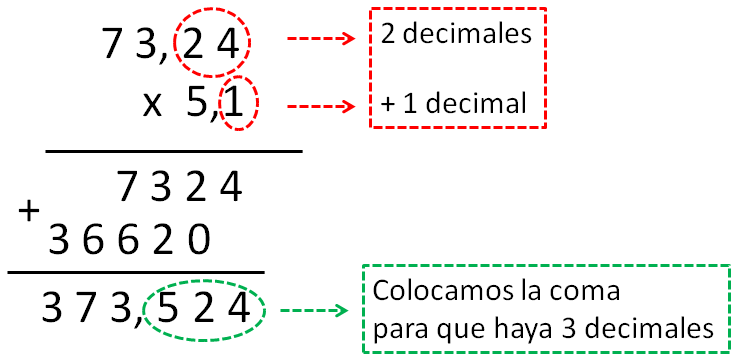
Resolvemos la multiplicación como hacemos normalmente con números enteros. Después, contamos las cifras que hay después de las comas de los dos factores. El resultado debe tener tantas cifras decimales como los dos factores juntos.

ACTIVIDAD # 15

INSTRUCTIVO 16

PLANO CARTESIANO CON NÚMEROS ENTEROS

El plano cartesiano es un sistema gráfico de referencia formado por dos rectas numéricas

que se cortan perpendicularmente.

(Se denomina cartesiano ya que fue René Descartes quien lo utilizó de manera formal por primera vez)
El punto de corte de las rectas se hace coincidir con el punto cero de las rectas y se conoce como origen del sistema. Al eje horizontal o de las abscisas se le asigna los números enteros de las equis ("x"); y al eje vertical o de las ordenadas se le asignan los números enteros enteros de las yes ("y").
Al cortarse las dos rectas dividen al plano en cuatro regiones, estas zonas se conocen como cuadrantes y se ordenan así.

Primer cuadrante "I" región superior derecha
Segundo cuadrante "II" región superior izquierda
Tercer cuadrante "III" región inferior izquierda
Cuarto cuadrante "IV" región inferior derecha
El plano cartesiano se utiliza para asignarle una ubicación a cualquier punto en el plano. En la gráfica anterior, por ejemplo se indica el punto +4 en las abscisas y +3 en las ordenadas.
El conjunto (4 , 3) se denomina "coordenadas" o "par ordenado" y del mismo modo se pueden ubicar otros puntos.

Otros ejemplos

Actividad #16

INSTRUCTIVO 17

RAZONES 

RAZÓN

La razón de dos cantidades o de dos números “a” y “b” es el cociente (resultado de la división) de estas cantidades.

Para comparar dos cantidades es necesario expresarlas en la misma unidad de medida.

La razón entre dos cantidades “a” y “b” la simbolizamos así.

a y leemos “a” es “b”

b

a: Se llama antecedente.

b: Se llama consecuente.

La razón es la comparación de dos magnitudes y se mide a partir del cociente (división) de esas dos cantidades. Es importante saber que esos dos valores tienen que estar en la misma unidad de medida.  Las razones parecen fracciones, pero se diferencian porque en las razones, tanto el numerador como el denominador,  pueden ser números no enteros.

Si se va a expresar la razón como fracción (a/b) o relación (a:b), esta debe reducirse hasta la forma más simple. Una razón también puede expresarse como un tanto por ciento.

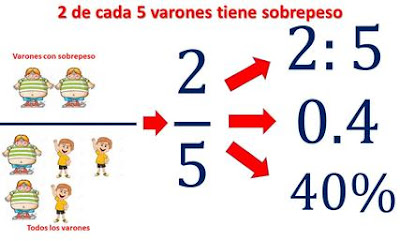
EJEMPLO: En la Escuela Primaria La Catrina, el quinto grado tiene solamente 5 alumnos y todos son varones.

De ellos, 2 tienen sobrepeso. ¿Cuál es la razón de niños con sobrepeso del quinto grado?

Total de niños varones:                 5        
Total de niños con sobrepeso:      2
Relación 2:5   

Se interpreta: 2 de cada 5 niños en la escuela La Catrina son obesos  

 ACTIVIDAD#17

INSTRUCTIVO #18

PROPORCIONES